NumPy 만으로 2-Layer Neural Network와 Backpropagation 구현해보기

 

 

 

1. 들어가며: 왜 직접 구현하는가?

 

딥러닝을 배우는 과정에서 우리는 10에 10은 TensorFlow나 PyTorch 같은 프레임워크를 사용한다

물론 이들 프레임워크는 강력하고 효율적이지만, 연산 과정이 내부적으로 감춰져 있기 때문에 신경망이 실제로 무엇을 하는지 직관적으로 이해하기 어렵기도 하다

 

그래서 이번 실습에서는 NumPy만 사용하여 2-layer Neural Network를 직접 구현하고, Forward Pass와 Backpropagation을 차근차근 살펴보았다

핵심 목표:  “코드가 돌아가는 이유를 이해하고, 모든 연산과 미분 과정이 눈에 보이도록 학습”

 

 

 

 

---

 

 

 

 

 

2. 데이터 준비: MNIST 손글씨 이미지

 

데이터 특징

• 28x28 픽셀 흑백 이미지
• Flatten하여 784차원 벡터로 변환
• 0~9 숫자 총 10개 클래스
• 라벨은 원-핫 인코딩(One-Hot Encoding)

import numpy as np
from tensorflow.keras.datasets import mnist
from tensorflow.keras.utils import to_categorical

(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(-1, 784) / 255.0
X_test = X_test.reshape(-1, 784) / 255.0

Y_train = to_categorical(y_train, 10)
Y_test = to_categorical(y_test, 10)

 

• 원래 X_train의 shape는 (60000, 28, 28)
• reshape로 0차원은 -1로 두고 뒤의 2-3차원 28x28 = 784로 주어서 3차원을 2차원으로 축소해준다
• 원래 Y_train은 데이터 개수만큼 정답값이 한줄로 있는, (60000,) 형태의 1차원 벡터이다
• 그러나 to_categorical을 사용해주면 정답값이 있는 인덱스를 1로 표기해주고 나머지는 0으로 표기하는, 원핫 인코딩 처리를 해준다
  • Y_train[0] : np.uint8(5), 숫자 5가 정답
  • to_categorical(Y_train, 10)[0] : array([0., 0., 0., 0., 0., 1., 0., 0., 0., 0.])

 

포인트

• 입력값 정규화(0~1)
• 원-핫 라벨 준비: Cross-Entropy 계산에 필요

 

 

 

 

 

3. 신경망 구조 설계

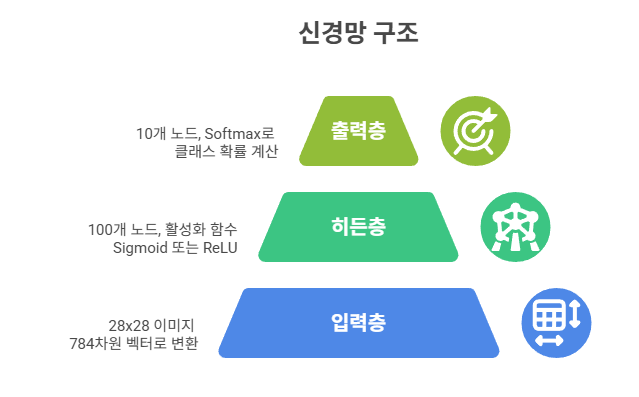
이번 신경망은 2개의 레이어를 가지는 다음과 같은 구조이다:

 

Input(784) -> Hidden Layer(100, Sigmoid or ReLU) -> Output Layer(10, Softmax)

• 입력층: 28x28 이미지를 784차원 벡터로 변환
• 히든층: 100개 노드, 활성화 함수 Sigmoid 또는 ReLU
• 출력층: 10개 노드, Softmax로 클래스 확률 계산

 

 

 

 

 

 

4. Weight 초기화 전략: Xavier vs He

 

Xavier Initialization

• Sigmoid나 Tanh에 적합

He Initialization

• ReLU 계열 활성화 함수에 적합

 

웨이트 초기화와 관련된 글을 이전에 정리한 적이 있다

 

혁펜하임의 Easy! 딥러닝 - 기울기 문제부터 배치 & 레이어 정규화까지

혁펜하임의 Easy! 딥러닝 - 기울기 문제부터 배치 & 레이어 정규화까지

 

 

혁펜하임 - AI DEEP DIVE

 

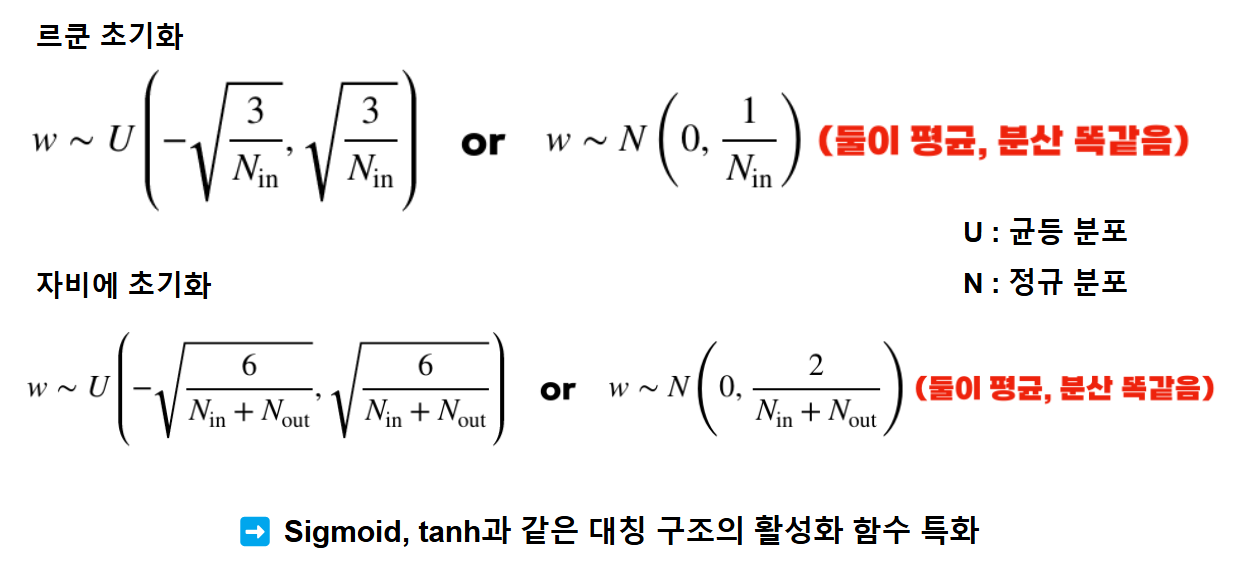
수식 그대로 구현해보면 아래의 코드와 같다

def init_params(input_dim, hidden_dim, output_dim, method="xavier"):
    if method == "xavier":
        limit1 = np.sqrt(6 / (input_dim + hidden_dim))
        limit2 = np.sqrt(6 / (hidden_dim + output_dim))
    elif method == "he":
        limit1 = np.sqrt(6 / input_dim)
        limit2 = np.sqrt(6 / hidden_dim)
    W1 = np.random.uniform(-limit1, limit1, (input_dim, hidden_dim)) # shape : (input_dim, num_hiddens) == (784, 100)
    b1 = np.zeros(hidden_dim) # shape : (num_hiddens,) == (100,)
    W2 = np.random.uniform(-limit2, limit2, (hidden_dim, output_dim)) # shape : (num_hiddens, num_classes) == (100, 10)
    b2 = np.zeros(output_dim) # shape : (num_classes,) == (10,)
    return {"W1": W1, "b1": b1, "W2": W2, "b2": b2}

 

초기화에 따라 학습 속도와 안정성이 크게 달라진다

 

 

 

5. Forward Pass 구현

 

핵심 수식

 

$$ z_{1} = XW_{1} + b_{1} $$

$$ a_1 = \text{activation}(z_1) $$

$$ z_2 = a_1W_2 + b_2 $$

$$ y = \text{softmax}(z_2) $$

 

 

주의

• 행렬 곱의 순서와 shape가 핵심
• Bias는 각 배치마다 브로드캐스팅됨
• Sigmoid는 0~1 범위, ReLU는 0~무한

출력값 확인

• Softmax 결과: 각 샘플별 10차원 확률 벡터

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def softmax(x):
    exp_x = np.exp(x - np.max(x, axis=1, keepdims=True))
    return exp_x / np.sum(exp_x, axis=1, keepdims=True)

def forward(X, params):
    z1 = X @ params["W1"] + params["b1"] # (32, 784) x (784, 100) => (32, 100) + (100,)
    a1 = sigmoid(z1) # (32, 100)
    z2 = a1 @ params["W2"] + params["b2"] # (32, 100) x (100, 10) => (32, 10) + (10,)
    y_hat = softmax(z2) # (32, 10)
    cache = {"X": X, "z1": z1, "a1": a1, "z2": z2, "y_hat": y_hat}
    return y_hat, cache

 

 

입력으로 들어오는 X와 가중치의 행렬 곱 연산 전에 shape가 정확히 일치하는지 잘 확인해야한다

 

 

6. Loss 계산: Cross-Entropy와 Softmax

 

수식

 

$$
L = - \frac{1}{n} \sum_{i=1}^{n} \sum_{c=1}^{C} y_{i,c} \log(\hat{y}_{i,c})
$$

 

미분

 

Softmax + Cross-Entropy의 조합에서 미분:

• 미분과정을 거치고 나면 아래처럼 예측 확률에서 실제 라벨을 빼는 간단한 형태로 나온다

$$
\frac{\partial L}{\partial z_i} = \hat{y}_i - y_i
$$

 

 

 

 

7. Backpropagation 구현

 

이해하는데 가장 오래 걸렸던 부분

 

$ z_{1} = XW_{1} + b_{1} $

$ a_1 = \text{activation}(z_1) $

$ z_2 = a_1W_2 + b_2 $

$ y = \text{softmax}(z_2) $

 

위의 Forward 에 있는 수식들 그대로 아래에서 위로 편미분을 해주면서 올라가면 된다

Loss → z2 → W2, b2 → a1 → z1 → W1, b1 순으로 진행한다

 

체인룰 적용

 

출력층:

$ y = \text{softmax}(z_2) $

• 예측값 y_hat에 대한 미분값은 바로 위의 Softmax + Cross-Entropy의 조합에서 미분을 참고하면 된다
• 그럼 예측값 - 실제값이라는 간단한 식을 코드로 구현하면 아래와 같다
• 배치 사이즈를 32이라 가정, 나오는 shape는 (32, 10)

dl_dz2 = y_hat - Y

 

 

히든층:

$ z_2 = a_1W_2 + b_2 $

• 해당 식에 있는 a1, W2, b2에 대해서 편미분을 통해 기울기를 계산한다
• 이 때 위의 출력층에서 구한 기울기와 행렬곱이 되기에 순서에 주의할 것
• 순서는 편미분을 했을 때 어디가 남는지를 잘 살펴보면 된다
• 예를 들어 dl_dW2 는 W2에 대해 편미분 했을 때 a1이 앞에 남고 뒤에 체인룰로 위에서 구한 기울기가 곱해지기에 
  dl_dW2 = a1.T @ dl_dz2 이런 식이 나오게 된다

Weight/편향 기울기:

dl_dW2 = a1.T @ dl_dz2
dl_db2 = np.sum(dl_dz2, axis=0)
dl_da1 = dl_dz2 @ W2.T

 

• 위에서 나온 a1의 shape는 (32, 100)
• dl_dz2의 shape는 (32,10)
• (32, 100) x (32, 10)  : shape 불일치 ❌ 따라서 앞의 a1을 트랜스포즈 취해준다
• (100, 32) x (32, 10) ✅

 

 

활성화 함수:

$ a_1 = \text{sigmoid}(z_1) $

 

Sigmoid의 경우

• 이전 글에서 보았듯이 시그모이드 함수를 미분하면 sigmoid(x) * (1 - sigmoid(x)) 라는 형태가 나온다
• a1은 시그모이드를 통과한 값. 따라서 편미분시 a1을 사용한다
• 위의 시그모이드 식을 z1에 대해 편미분하면 체인룰에 의해 이전 기울기 dl_da1과 시그모이드 미분, sigmoid(x) * (1 - sigmoid(x)) 이 곱해진 형태가 나오게 된다

dl_dz1 = dl_da1 * a1 * (1 - a1)

 

 

 

ReLU의 경우

• ReLU는 양수는 y = x, 0과 음수는 0으로 만들기 때문에 이전 기울기값이 음수냐 양수냐에 따라 기울기가 전달되거나 0으로 전달되지 않는다
• 양수라면 y = x의 기울기는 1, 이전 기울기가 그대로 전달되며 0이하일 경우 0으로 만든다
• z1 > 0 이라는 조건에서 bool로 0, 1을 곱하여 필터링을 해주는 식이다

dl_dz1 = dl_da1 * (z1 > 0)

 

포인트

• 각 행렬 곱과 차원 확인
• 활성화 함수 미분 적용 필수

 

위의 내용들을 정리하면 아래와 같다

def backward(Y, cache, params):
    m = Y.shape[0]
    dz2 = (cache["y_hat"] - Y) / m
    dW2 = cache["a1"].T @ dz2
    db2 = np.sum(dz2, axis=0)

    da1 = dz2 @ params["W2"].T
    dz1 = da1 * cache["a1"] * (1 - cache["a1"])  # sigmoid 미분
    dW1 = cache["X"].T @ dz1
    db1 = np.sum(dz1, axis=0)

    return {"dW1": dW1, "db1": db1, "dW2": dW2, "db2": db2}

 

 

 

 

 

 

 

8. Gradient Descent를 통한 학습

Mini-batch 학습

• Batch size: 32
• 학습률: 0.001 

업데이트

• 자비에 또는 카이밍 허 초기화를 통해 설정한 가중치에서 역전파를 통해 각각 구했던 기울기에 학습률을 곱하여 뺌으로써 업데이트를 해준다

def update_params(params, grads, lr=0.1):
    for key in params.keys():
        params[key] -= lr * grads["d" + key]
    return params

---
self.params['W2'] = self.params['W2'] - lr * grad['dl_dW2']
self.params['b2'] = self.params['b2'] - lr * grad['dl_db2']
self.params['W1'] = self.params['W1'] - lr * grad['dl_dW1']
self.params['b1'] = self.params['b1'] - lr * grad['dl_db1']

• 여기서 params의 key들은 가중치 초기화를 해서 설정한 W1, W2, b1, b2

 

 

9. 모델 검증 (Evaluate)

 

위에서 순전파-역전파, 가중치 업데이트 뿐 아니라 epoch마다 모델의 지속적인 성능 확인이 필요하다

순전파를 통해 얻은 예측값과 실제값만 있다면 어느 정도의 정확도를 가지는지 측정할 수 있다

 

def evaluate(Y, Y_hat):
    # Accuracy 계산
    pred = np.argmax(Y_hat, axis=1)
    true = np.argmax(Y, axis=1)
    accuracy = np.mean(pred == true)
    return accuracy

 

앞에서 우리는 to_categorical 메서드를 통해 라벨값들을 10개 중 위치한 인덱스를 표시하는 원-핫 인코딩을 해주었다

 

1. np.argmax로 예측값 변환

Y_hat은 모델 출력으로, softmax를 통해 각 클래스에 대한 확률 분포 형태이다
예를 들어, 한 샘플의 Y_hat이 아래와 같다면:

y_hat_sample = [0.05, 0.01, 0.88, 0.03, 0.01, 0.01, 0.01, 0.0, 0.0, 0.0]

• softmax 확률에서 가장 높은 값(0.88)의 인덱스를 예측 클래스라고 판단
• np.argmax(y_hat_sample) → 2 (클래스 2를 예측)

2. 정답 라벨 변환

Y는 원-핫 인코딩 형태로 되어 있다. 예를 들어 클래스 2가 정답이면:

Y_sample = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]

• np.argmax(Y_sample) → 2 (정답 클래스)

3. 비교 및 평균

pred == true

• 예측 클래스와 실제 클래스가 일치하면 True, 아니면 False
• 여러 샘플을 처리할 때 np.mean()를 사용하면 전체 일치 비율 = accuracy

예시:

pred	true	pred == true
2	2	True
0	0	True
4	3	False

• Accuracy = (2/3) = 0.6667

 

 

 

 

 

 

---

 

 

 

 

마무리

이번 내용은 사실상 이전에 정리한 글, "MSE Loss와 시그모이드에서의 역전파 이해하기" 와 비슷한 내용임에도 불구하고 이해하는데 오랜 시간이 걸렸다

이전에는 역전파 일부만 다루었다면 이번에는 간단한 데이터를 가져와서 가중치와 편향부터 직접 설정하고 이걸 순전파와 역전파를 할 때 어떤 요소들을 적절하게 사용해야하는지, 더 확장된 내용이었기에 애를 먹었던 것 같다

 

뒤의 공부들이 밀렸지만.. 여기서 배운 것들이 정말 기본적이고 근본이 되는 내용이기에 시간이 오래 걸리더라도 최대한 이해하고 넘어가는 것이 중요하다고 생각하여 정리해보았다

 

 

 

 

 

 

 

 

참고자료

 

https://humankind.tistory.com/59

[밑바닥딥러닝] 10. 오차역전파법(backpropagation) 구현(1)

 

이 글 내용도 괜찮았다. 밑바딥을 보고 싶지만.. 내용이 많이 겹치기도 하고 다 볼 수는 없어서 패스. 대신 혁펜님 Easy 딥러닝 책 병행하면서 추석 전까지는 꼭 다보자