MSE Loss와 시그모이드에서의 역전파 이해하기

 

 

 

최근에 공부하면서 가장 헷갈렸던 부분이 바로 손실 함수의 미분, 그리고 그 이후 시그모이드 미분 → 가중치 업데이트 과정이었다처음에는 error = y - pred 같은 코드가 왜 맞는지, 왜 X.T @ error 같은 연산이 나오는지 이해가 잘 안 갔다

그래서 순전파와 역전파 과정을 하나씩 풀어가면서 정리했다

 

 

 

1. 순전파 (Forward Pass)

 

순전파는 입력 데이터를 모델에 넣어서 예측값과 손실 (loss)을 계산하는 과정이다.

 

 

1. 입력 데이터와 정답
$ X = [[1, 2], [3, 4], [5, 6]] $
$ y = [1, 0, 1] $

 

 

 

2. 가중치와 편향 초기값
$ beta = [0, 0] $

$ b = 0 $

 

 

 

3. 로짓 계산
$$ z=Xβ+b $$

 

 

 

4. 시그모이드 활성화
$$ \hat{y} = \sigma(z) $$

예시 값:  $ [0.8, 0.3, 0.4] $

 

 

 

5. 손실 (MSE)
$$ L = \frac{1}{n}\sum (y - \hat{y})^2 $$

 

 

# ---------- 활성화 함수 ----------
def sigmoid(z):
    return 1.0 / (1.0 + np.exp(-z))

# ---------- 손실 함수 ----------
def mse_loss(y_true, y_pred):
    return np.mean(0.5 * (y_true - y_pred)**2)

def forward(X, beta, b):
    """
    Forward pass:
      z = X @ beta + b
      y_pred = sigmoid(z)
      loss = MSE(y, y_pred)
    """
    z = X @ beta + b
    y_pred = sigmoid(z)
    return z, y_pred

 

 

 

여기까지는 이해하는데 무리가 없었다

입력 데이터 X가 가중치 w와 편향 b, $ y = wx + b $ 연산을 거쳐 나온 값이 시그모이드를 통과하면서 0과 1사이의 확률값, 예측값이 나온다

그리고 이 예측값과 실제값 사이의 MSE 손실 함수를 통해 loss값이 나오는 가장 기본적인 형태

코드로 살펴보아도 직관적이고 쉽게 이해할 수 있다

 

 

 

 

 

 

 

2. 역전파 (Backward Pass)

 

이제 손실값을 가중치와 편향에 대해 미분해서 기울기(gradient) 를 구한다

이때 체인룰(연쇄법칙) 을 이용한다

 

1. 손실 → 예측값

$$ \frac{\partial L}{\partial \hat{y}} = ( \hat{y} - y) $$

예시: [0.2, -0.3, 0.6]

 

 

2. 예측값 → 로짓 (시그모이드 미분)
$$ \frac{\partial \hat{y}}{\partial z} = \hat{y}(1 - \hat{y}) $$
예시: [0.16, 0.21, 0.24]

 

 

3. 손실 → 로짓
$$ \frac{\partial L}{\partial z} = ( \hat{y} - y) \cdot \hat{y}(1 - \hat{y}) $$
예시: [0.032, -0.063, 0.144]

 

 

4. 로짓 → 가중치

로짓: $ z = X\beta + b $

미분: $ \frac{\partial z}{\partial \beta} = X $

따라서: $ \beta\_{grad} = X^T error $

계산 결과: [-0.563, -0.676]

 

 

5. 로짓 → 편향
$$ b\_{grad} = -\text{mean}(error) = -0.0377 $$

 

 

# ---------- 역전파 (Backward) ----------
def backward(X, y_true, y_pred):
    """
    Backward pass (MSE + sigmoid):
      dL/dy = (y_pred - y_true)
      dL/dz = dL/dy * y_pred * (1 - y_pred)
      dL/dbeta = X.T @ dL/dz
      dL/db = mean(dL/dz)
    """
    dL_dy = y_pred - y_true                 # (N,1)
    dL_dz = dL_dy * y_pred * (1 - y_pred)   # (N,1)
    beta_grad = X.T @ dL_dz                 # (f,1)
    b_grad = np.mean(dL_dz)                 # scalar
    return beta_grad, b_grad

 

 

위의 내용과 코드가 이해가는가? 난 모르겠다...

왜 역전파를 구하는데 입력 데이터 X, 타겟값 y_true 랑 예측값 y_pred 이 들어가는지.. 

왜 코드는 y_pred = y_true가 나오는지... 아래에선 왜 또 dL/dy * y_pred * (1 - y_pred) 이렇게 곱해주고 있는지...

beta_grad가 기울기인거 같은데 왜 X에 트랜스포즈를 해주는데? 으아아... 😇

 

저 코드와 순서, 그리고 위의 수식들을 이해하려면 먼저 체인룰로 어떤 형태로 이루어져 있는지를 이해 해야한다

자세한 설명은 하지 않고, 어떤 형태인지만 살펴보겠다

 

 

 

 

먼저, 우리가 구해야하는 기울기는 beta에 대한 기울기이다

하지만 순전파에서 여러 단계를 거치듯이, 역전파에서 beta까지 바로 가기에는 중간에 여러 단계들이 존재한다

 

순전파를 일련의 과정으로 보기좋게 정리하면 아래와 같다

 

순전파 (forward pass)

입력 $X$ 를 받아서 선형 결합 $z=Xβ+b$

$z$ → 시그모이드 통과 → 예측값 $\hat{y} = \sigma(z)$

손실 $L = \text{loss}(y, \hat{y})$ : $L = \frac{1}{2}(y - \hat{y})^2$

 

선형 함수 하나 거치고 활성화 함수도 하나 거치고 그리고 손실 함수도 거치네?

✅ 그대로 거꾸로 하나씩 거치면 된다. 손실함수 - 활성화 함수 - 선형 함수 순으로.

 

 

역전파 (backward pass)

손실 $L$ 을 파라미터 $(β,b)$ 에 대해 미분 → gradient 구하기

체인룰을 각 단계별로 풀어쓰면 아래와 같다

 

$$  \frac{\partial L}{\partial \beta} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z} \cdot \frac{\partial z}{\partial \beta} $$

 

 

오.. 하나씩 볼까??

 

 

$$  \frac{\partial L}{\partial \beta} $$

• 오차, 손실함수 L에 대한 가중치 beta 편미분값
• 지금 나온 오차에 대해서 가중치 기울기를 계산하겠어요 하는 것

 

 

 

$$  \frac{\partial L}{\partial \hat{y}} $$

• 하지만 beta에 대해서 바로 계산할 수는 없다
• 그래서 가장 가까이에 연결되어 있는 y-hat 값에 대해 미분값을 구한다
• 순전파에서 입력이 시그모이드를 통과한 확률, 예측값이고 출력은 loss값
• 이걸 거꾸로 뒤집으면 된다. 식은 손실함수! 위에 MSE 식을 미분한다!!!

그럼 요 MSE 식이 미분되어서

$$ L = \frac{1}{2}\sum (y - \hat{y})^2 $$

 

아래처럼 나오게된다 ( 미분 과정은 생략.. )

 

$$ \frac{\partial L}{\partial \hat{y}} = ( \hat{y} - y) $$

그럼 이제 감이 잡힌다!! 체인룰에 있는거 하나씩 어떤 식인지 확인하고 미분해줘서 싹 곱해주면 된다!!! 

y-hat - y..? 어... 이거 어디서 봤는데..? 

dL_dy = y_pred - y_true

 

 

 

 

$$   \frac{\partial \hat{y}}{\partial z}  $$

• 순전파에서 이 부분이 뭐였을까?
• 선형 함수 z를 거쳐 나온 값이 시그모이드를 통과하여 y-hat이 나온 부분이다
• 그럼 여기는 시그모이드 함수에 대해 미분해주면 된다

 

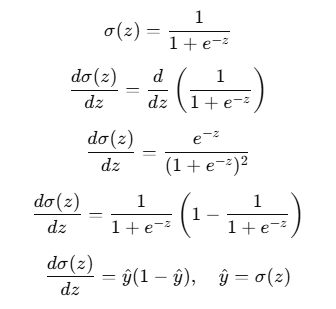
시그모이드를 거치면 나오는 값이 y-hat이니까 예측값.. 어..?

y_pred * (1 - y_pred)

 

 

 

 

$$   \frac{\partial z}{\partial \beta} $$

• 드디어 우리가 목표로 했던 beta까지 왔다. 이번에는 선형함수이다 
• 위의 식을 다시 확인해보면 $ z=Xβ+b $
• 이제 z를 β 에 대해 미분하면 무엇이 남는지 살펴보자.

 

$$   \frac{\partial z}{\partial \beta}  = X $$

 

• 선형함수이기 때문에 입력값 X가 그대로 남는다. 그래서 역전파에서 기울기를 계산할 때 입력 데이터 X가 사용되는 것이다
• 하지만 그대로 곱할 수는 없다
• 하지만 여러 샘플을 배치 단위로 학습한다고 가정하면, 지금까지 계산한 기울기 값들은 벡터나 행렬 형태로 쌓여 있다.
• 이 상태에서 체인룰로 순차적으로 곱해진 기울기에 마지막 XXX를 곱하려면, shape(행렬 차원)을 맞춰주어야 한다.
• 따라서 트랜스포즈를 사용해 행렬곱을 수행하게 되는 것이다

b_grad = np.mean(dL_dz)

 

 

이렇게 구한 기울기값은 아래에 학습률과 곱해서 기존의 가중치에 업데이트해주면 된다!

 

 

 

++추가로 손실함수 L에 대해 y-hat 미분했을 때 y_true - y_pred로 코드를 작성한다면 아래에서 마이너스 붙여주면 똑같다

종종 혼용되는 경우가 있으니 부호 주의할 것.

dL_dy = y_true - y_pred                 # (N,1)
dL_dz = dL_dy * y_pred * (1 - y_pred)   # (N,1)
beta_grad = - X.T @ dL_dz                 # (f,1)

 

 

3. 파라미터 업데이트 (SGD)

 

학습률 $η=0.1 $ 일 때,

• 가중치 업데이트:
  $ \beta \leftarrow \beta - \eta * \beta\_{grad} $
• 편향 업데이트:
  $ b \leftarrow b - \eta * b\_{grad} $

업데이트 결과:

β = [0.0563, 0.0676]
b = 0.00377

 

 

 

4. 마무리

• 순전파: 입력 데이터 → 가중치/편향 → 로짓 → 시그모이드 → 예측값 → 손실
• 역전파: 손실 → 예측값 → 시그모이드 → 로짓 → (X, 가중치, 편향)
• 결국 beta_grad =  X.T @ error는 체인룰을 끝까지 적용한 결과다.
• 여기서 X가 등장하는 이유는, 로짓 $ z=Xβ+b $ 에서 가중치에 대한 미분값이 바로 X이기 때문이다.

 

 

 

 

 

---

 

 

 

 

 

 

이번에 공부하면서 코드 보는데 뭐지...? 싶어서 어제오늘 거의 이틀 동안 이 부분만 계속 이해하려고 찾아본 것 같다

“왜 X.T @ error인지 모르겠다” 싶었던 게, 사실은 순전파 식을 역으로 추적해가면서 체인룰을 적용한 결과였다

이 과정을 이해하니까 수학적인 부분이 어떻게 코드로 구현되었는지 잘 알게 되었다

솔직히 시간을 생각보다 많이 쓰게 되서 다른 공부들도 밀리긴 했지만... 예전에 대충 보고 넘어갔던 개념을 이해할 때까지 파보고 이해했다는 점에서 충분의 유의미한 시간들이었다!